Using Perplexity to eliminate known data points
In this guide, we're covering the most reliable metric to determine how important are data points in the cluster for training an LLM.
In the last blog, we taught you how to reduce the size of the dataset simply by just clustering the embeddings.
Now we will expand on that and use a more reliable metric to determine how important are data points in the cluster for training an LLM. A simple way to think of it like using a metric to determine if an LLM is already familiar with the data points from a cluster.
How to Use Perplexity to Evaluate LLM Performance?
One way to measure this is using the perplexity score. Perplexity is a metric used to evaluate the performance of language models, particularly in the context of natural language processing tasks. It measures how well a model predicts a sample by calculating the inverse probability of the true sequence, normalized by the number of words.
A lower perplexity score indicates that the model is better at predicting the next word in a sequence, meaning it has a higher degree of confidence and accuracy. Conversely, a higher perplexity score suggests that the model struggles to predict words, indicating less fluency or coherence in its output. This metric is commonly used to compare language models or fine-tuned models to assess improvements in text generation.
Now let us see a simple example on how to eliminate irrelevant training data using perplexity score.
First step is to load the dataset we are going to use for training
from datasets import load_dataset
texts = load_dataset("RaagulQB/CodeExercise-Python-27k-copy", split="train")["Instruction"]Load any embedding model of your choice from sentence transformers we have used all-MiniLM due to its speed.
from sentence_transformers import SentenceTransformer
model = SentenceTransformer('all-MiniLM-L6-v2',device='cuda')Embedding the training column
import tqdm
embeddings = []
for text in tqdm.tqdm(texts):
embeddings.append(model.encode(text))
Next step is to cluster the dataset into a fixed number of clusters one can opt to use agglomerative clustering as well.
from sklearn.mixture import GaussianMixture
num_clusters = 15 # Set the number of clusters
gmm = GaussianMixture(n_components=num_clusters, random_state=0)
gmm.fit(embeddings)
# Get cluster assignments
cluster_assignments = gmm.predict(embeddings)Next step is to assign each data point to a cluster id using the cluster assignments given by GMM.
cluster_dict = {}
for idx, label in enumerate(cluster_assignments):
if label not in cluster_dict:
cluster_dict[label] = []
cluster_dict[label].append(texts[idx])The next step is to consider a small sample from each cluster to calculate the perplexity score. We have taken 10% of the points randomly you can use your own logic here as well
import random
# New dictionary to store the thinned clusters
thinned_cluster_dict = {}
for label, texts in cluster_dict.items():
if label == -1:
thinned_cluster_dict[label] = texts
continue
# Calculate 10% of the original size, ensuring at least 1 item is selected
thinned_size = max(1, len(texts) // 10)
thinned_texts = random.sample(texts, thinned_size)
thinned_cluster_dict[label] = thinned_texts
# Output the thinned cluster dictionary
for label, texts in thinned_cluster_dict.items():
print(f"Cluster {label}:")
print(len(texts))
Next step is to create a sample dataset for each cluster using the samples we formed
# Initialize a new dictionary to store the filtered datasets
filtered_datasets_dict = {}
# Loop through each cluster in thinned_cluster_dict
for label, texts in thinned_cluster_dict.items():
combined_values_set = set(texts)
# Define the filtering function for each cluster
def filter_passages(example):
return example['Instruction'] in combined_values_set
# Apply the filter to the dataset and store it in the new dictionary
filtered_datasets_dict[label] = dataset.filter(filter_passages)
# The filtered_datasets_dict now contains a filtered dataset for each clusterOnce this is done the next steps are relatively simple,
- Load the model and tokenizer and model you wish to fine-tune.
- Calculate the perplexity of the sample datasets.
- Fix a threshold and eliminate clusters that have perplexity less than that threshold.
base_model = "google/gemma-2-2b-it"
tokenizer = AutoTokenizer.from_pretrained(base_model)
def format_chat_template(row):
row_json = [{"role": "user", "content": row["Instruction"]},
{"role": "assistant", "content": row["Response"]}]
row["text"] = tokenizer.apply_chat_template(row_json, tokenize=False)
return row
# Apply the function to each dataset in the dictionary
for label, dataset in filtered_datasets_dict.items():
filtered_datasets_dict[label] = dataset.map(format_chat_template)
model = AutoModelForCausalLM.from_pretrained(base_model,device_map="auto")
import torch
device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')
def add_perplexity_column(example):
"""
Calculate the perplexity score for a given text example and add it to the dataset.
Args:
example (dict): The input example containing the 'text' key.
Returns:
dict: The updated example with an additional 'perplexity' key.
"""
text = example['text']
inputs = tokenizer(text, return_tensors='pt')
# Move the input tensors to the same device as the model
input_ids = inputs['input_ids'].to(device)
attention_mask = inputs.get('attention_mask', None)
if attention_mask is not None:
attention_mask = attention_mask.to(device)
# Calculate the loss (negative log-likelihood)
with torch.no_grad():
outputs = model(input_ids, attention_mask=attention_mask, labels=input_ids)
loss = outputs.loss
# Perplexity is the exponential of the loss
perplexity = torch.exp(loss).item()
example['perplexity'] = perplexity
return examplefor label, dataset in filtered_datasets_dict.items():
filtered_datasets_dict[label] = dataset.map(add_perplexity_column)# Compute and print the average perplexity for each dataset
for label, dataset in filtered_datasets_dict.items():
# Extract the perplexity scores from the dataset
perplexities = dataset['perplexity']
# Compute the average perplexity
avg_perplexity = sum(perplexities) / len(perplexities)
# Print the result
print(f"Cluster {label}: Average Perplexity = {avg_perplexity:.4f}")# List to store cluster IDs with average perplexity >= 2.5
retained_cluster_ids = []
# Loop through each dataset in the dictionary
for label, dataset in filtered_datasets_dict.items():
# Extract the perplexity scores
perplexities = dataset['perplexity']
# Compute the average perplexity
avg_perplexity = sum(perplexities) / len(perplexities)
# Keep the cluster ID only if the average perplexity is >= 2.5
if avg_perplexity >= 3:
retained_cluster_ids.append(label)
# Print the retained cluster IDs
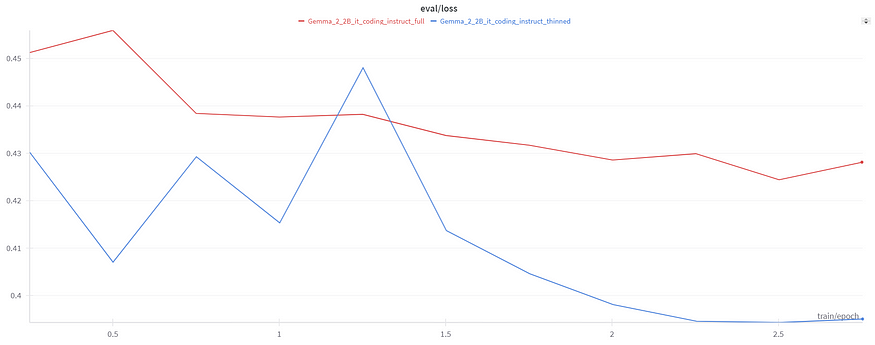
print("Retained Cluster IDs:", retained_cluster_ids)Our original dataset had about 27K rows e were able to reduce it to 16K rows which was around 40% reduction in size on fine-tuning Gemma-2–2B-it on both the datasets we were even able achieve a slightly better performance on the model trained on the thinned dataset.